Method of Indicators - Data 140 Textbook

# HIDDEN
from datascience import *
from prob140 import *
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
%matplotlib inline
import math
from scipy import stats
from scipy import misc

This is a powerful method for finding expected counts. It is based on the observation that among $n$ trials, the number of “good” results can be counted by first coding each “good” result as 1 and each of the other results as 0, and then adding the 1’s and 0’s.

If $N$ is the total number of good results among $n$ trials, then

N = I_1 + I_2 + \cdots + I_n

where for each $j$ in the range 1 through $n$ , the random variable $I_j$ is the indicator of “the result of the $j$ th trial is good”.

Now recall that if $I_A$ is the indicator of an event $A$ , then $E(I_A) = P(A)$ . That is, the expectation of an indicator is the probability of the event that it indicates.

So

\begin{align*} E(N) &= E(I_1) + E(I_2) + \cdots + E(I_n) \\ &= P(\text{result of Trial } 1 \text{ is good}) + P(\text{result of Trial } 2 \text{ is good}) + \cdots + P(\text{result of Trial } n \text{ is good}) \\ \end{align*}

It is important to note that the additivity works regardless of whether the trials are dependent or independent.

from IPython.display import YouTubeVideo
YouTubeVideo('hOIcQUYUNsM')

Loading...

8.5.1Expectation of the Binomial¶

Let $X$ have the binomial $(n, p)$ distribution. Then $X$ can be thought of as the number of successes in $n$ i.i.d. Bernoulli $(p)$ trials, and we can write

X = I_1 + I_2 + \cdots + I_n

where for each $j$ in the range 1 through $n$ , $I_j$ is the indicator of “Trial $j$ is a success”. Thus

\begin{align*} E(X) &= E(I_1) + E(I_2) + \cdots + E(I_n) ~~~~ \text{(additivity)} \\ &= np ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \text{(}E(I_j) = p \text{ for all } j \text{)} \end{align*}

Examples of use:

The expected number of heads in 100 tosses of a coin is $100 \times 0.5 = 50$ .
The expected number of heads in 25 tosses is 12.5. Remember that the expectation of an integer-valued random variable need not be an integer.
The expected number of times green pockets win in 20 independent spins of a roulette wheel is $20 \times \frac{2}{38} = 1.053$ , roughly.

k = np.arange(11)
probs = stats.binom.pmf(k, 10, 0.75)
bin_10_75 = Table().values(k).probabilities(probs)
Plot(bin_10_75, show_ev=True)
plt.title('Binomial (10, 0.75)');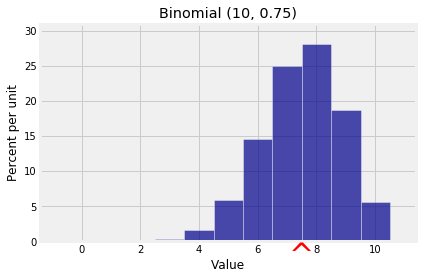

Notice that we didn’t use independence. Additivity of expectation works whether or not the random variables being added are independent. This will be very helpful in the next example.

YouTubeVideo('lz-UuQqvUOE')

Loading...

8.5.2Expectation of the Hypergeometric¶

Let $X$ have the hypergeometric $(N, G, n)$ distribution. Then $X$ can be thought of as the number of good elements in $n$ draws made at random without replacement from a population of $N = G+B$ elements of which $G$ are good and $B$ bad. Then

X = I_1 + I_2 + \cdots + I_n

where for each $j$ in the range 1 through $n$ , $I_j$ is the indicator of “Draw $j$ results in a good element”. Thus

\begin{align*} E(X) &= E(I_1) + E(I_2) + \cdots + E(I_n) ~~~~ \text{(additivity)} \\ \\ &= n\frac{G}{N} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \text{(}E(I_j) = \frac{G}{N} \text{ for all } j \text{ by symmetry)} \end{align*}

This is the same answer as for the binomial, with the population proportion of good elements $G/N$ replacing $p$ .

Examples of use:

The expected number of red cards in a bridge hand of 13 cards is $13 \times \frac{26}{52} = 6.5$ .
The expected number of Independent voters in a simple random sample of 200 people drawn from a population in which 10% of the voters are Independent is $200 \times 0.1 = 20$ .

These answers are intuitively clear, and we now have a theoretical justification for them.

# Number of hearts in a poker hand 
N = 52
G = 13
n = 5
k = np.arange(6)
probs = stats.hypergeom.pmf(k, N, G, n)
hyp_dist = Table().values(k).probabilities(probs)
Plot(hyp_dist, show_ev=True)
plt.title('Hypergeometric (N=52, G=13, n=5)');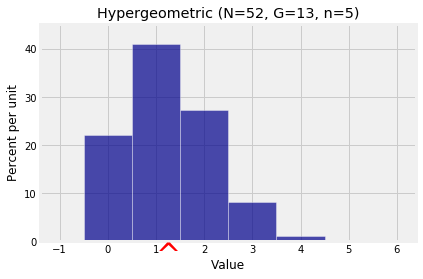

Answer

(a) 4 by the binomial expectation formula

(b) 4 by the hypergeometric expectation formula

8.5.3Number of Missing Classes¶

A population consists of four classes of individuals, in the proportions 0.4, 0.3, 0.2, and 0.1. A random sample of $n$ individuals is chosen so that the choices are mutually independent. What is the expected number of classes that are missing in the sample?

If $M$ is the number of missing classes, then

M = I_1 + I_2 + I_3 + I_4

where for each $j$ , $I_j$ is the indicator of “Class $j$ is missing in the sample”.

For Class $j$ to be missing in the sample, all $n$ selected individuals have to be from the other classes. Thus

E(M) = E(I_1) + E(I_2) + E(I_3) + E(I_4) = 0.6^n + 0.7^n + 0.8^n + 0.9^n

The four indicators aren’t independent but that doesn’t affect the additivity of expectation.

YouTubeVideo('mxj4Gr_QUCM')

Loading...

Answer

(ii)

8.5 Method of Indicators

8.5.1Expectation of the Binomial¶

8.5.2Expectation of the Hypergeometric¶

8.5.3Number of Missing Classes¶